Çinli Araştırmacılar, Kuantum Bilgisayar kullanarak, 2048-bit RSA Şifrelemesini kırdıkları konusunda bir yayın yaptılar.
RSA (Rivest–Shamir–Adleman) algoritması güvenli data iletiminde kullanılan/kullandığımız oldukça yaygın bir algoritma. RSA, Ron Rivest, Adi Shamir ve Leonard Adleman tarafından 1977 yılında yayınlandı. 1973 yılında İngiliz matematikçi Clifford Cocks tarafından İngiliz İletişim Merkez (GCHQ) tarafından geliştirilen algoritmanın gizliliği 1997 kaldırıldı.
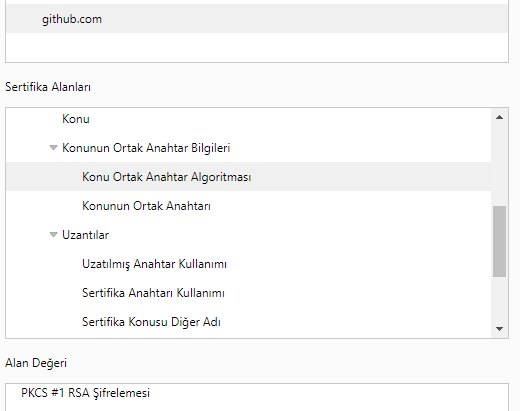
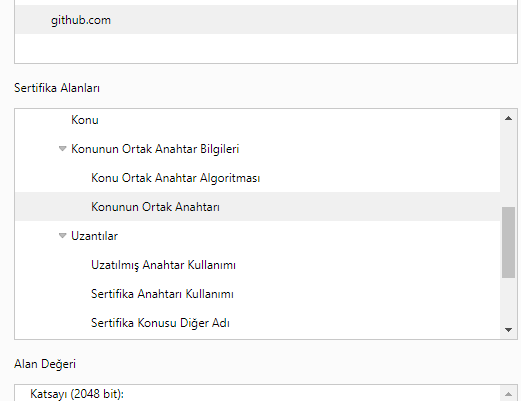
RSA algoritması oldukça yaygın olarak kullanılmaktadır. Güncel bir sitede (örneğin https://github.com/) Ortak anahtar bilgilerine baktığınızda Algoritmanın RSA ve Ortak Anahtarın 2048-bit seviyesinde olduğu görülebilir. Bunun anlamı bu algoritma kırıldığında, ortadaki adam saldırısı ile kullanıcı adı ve parola dahil verilere erişilebilir, değiştirilebilir ve tekrar iletilebilir.
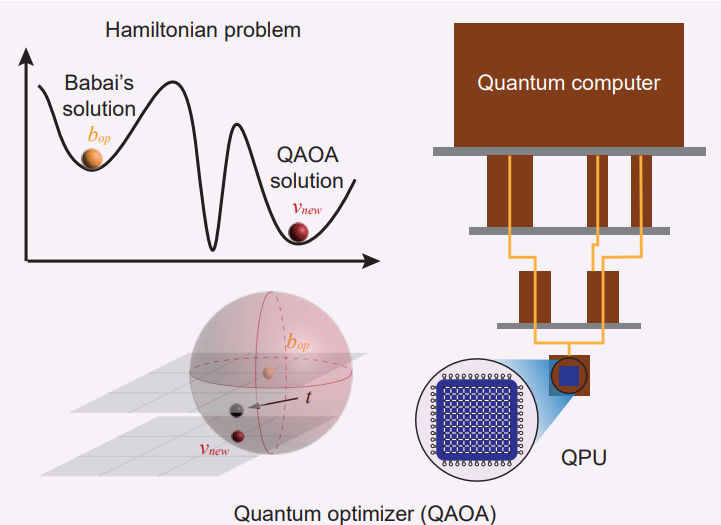
Yayın içeriği incelendiğinde; Araştırma için kullanılan Kuantum Bilgisayarın, sivil olarak temin edebilecek 10-qubit (qbit veya kubit) hesap yapabilen bir seviyede olduğu görülüyor. Ancak önemli bir detay, kırılma durumu 372-qubit seviyesinde gerçekleşebileceği yayından anlaşılıyor (hipotez).

Bu yazı yazıldığında, ilgili makale arXiv üzerinde yayınlandığı için henüz karşıt bir doğrulama veya yalanlama gelmemiştir.
Konu ile ilgili bir google tartışma grubu oluşturulmuş. Grup özellikle “2048-bitlik tamsayıları çarpanlarına ayırma yönteminin aslında klasik yöntemlerden daha hızlı olup olmadığını” sorguluyor.
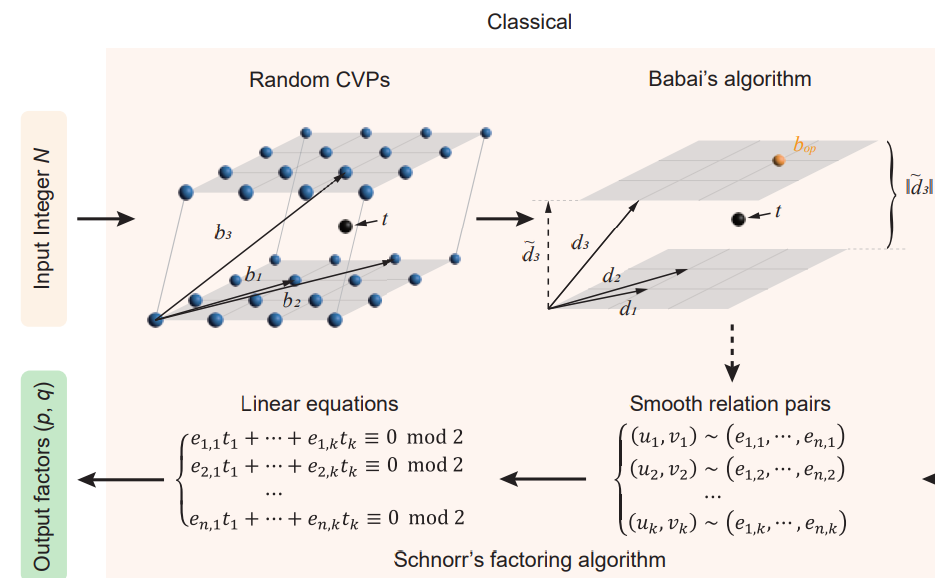
Kriptografi uzmanı Bruce Schneier‘ın incelemesinde, kullanılan metodun Alman matematikçi Peter Schnorr‘un tartışmalı bir makalesini dayandığı ve daha büyük boyutlu analizlerde çözümden uzaklaştığını yorumluyor.
Schneier; “Bu gün kullandığımız anahtar boyutlarında verinin kırılabilmesi için milyonlarca qbitlik büyük bir kuantum bilgisayarı gerekir. Araştırmacılar, klasik indirgeme tekniklerini bir kuantum yaklaşık optimizasyon algoritması ile birleştirmiş. Bu durumda yalnızca 372-qbit’lik bir kuantum bilgisayara ihtiyaç duydukları anlamına gelir ki bu, bugün mümkün için elde edilmesi mümkün bir değer. Örneğin IBM Osprey, 433 qbit‘lik bir kuantum bilgisayardır.
Çinli grubun çalışacak o kadar büyük bir kuantum bilgisayarı yokmuş. 10-qbitlik bir kuantum bilgisayarı kullanarak 48 bitlik sayıları çarpanlara ayırabilmişler. Ve bunun gibi bir şeyi 50 kat büyütürken her zaman potansiyel sorunlar olsa da, bariz engeller de yoktur!
Dürüst olmak gerekirse, makalenin çoğu – hem indirgeme matematiği hem de kuantum fiziği – beni aşıyor. Ve Çin hükümetinin bu araştırmayı neden sınıflandırmadığına dair rahatsız edici bir soru var.
Roger Grimes e-posta ile bana şunları iletti: “Görünüşe göre, daha önce klasik bilgisayarları kullanarak geleneksel asimetrik şifrelemeyi kırabildiğini açıklayan başka bir araştırmacı olmuş… ama eleştirmenler onun algoritmasında bir kusur bulmuş ve o araştırmacı makalesini geri çekmek zorunda kalmış. Ancak bu Çinli ekip, algortimanın küçük kuantum bilgisayarlar tarafından çözülebileceğini fark ettmiş. Bu yüzden test ettiler ve işe yaradı.”
Algoritmayla ilgili sorunlardan biri, Claus Schnorr’un yakın tarihli bir makalesine dayanmasıdır. Bu tartışmalı bir makale; ve özette “bu, RSA kripto sistemini yok eder” iddiasına rağmen, Schnorr’un algoritması, daha küçük modüllerle iyi çalışıyor – Çinli grubun test ettiğiyle yaklaşık aynı sırada – ancak daha büyük boyutlarda başarısız oluyor. Bu noktada, kimse nedenini anlamıyor. Çin gazetesi, kuantum tekniklerinin bu sınırlamayı aştığını iddia ediyor (Grimes’ın yorumunun arkasında yatan şeyin bu olduğunu düşünüyorum) ancak herhangi bir ayrıntı vermiyorlar ve bunu daha büyük modüllerle test etmediler. Dolayısıyla, Çin gazetesinin ölçeklenmeyen bu Schnorr tekniğine bağlı olduğu doğruysa, bu Çin makalesindeki teknikler de ölçeklenmeyecektir. (Öte yandan, ölçeklenirse, o zaman açık anahtarlı şifreleme sistemini de bozduğunu düşünürüm.) Ancak bu, IBM kuantum bilgi işlem çalışanlarının şu anda test edebileceği bir şey. Az önce bir muhabir bana bu konudaki hislerimi sordu. Bunun RSA’yı bozacağını düşünmediğimi söyledim.
Yeni makalede yazarlar, bir NISQ (yani, hataya dayanıklı olmayan) kuantum bilgisayar kullanarak yakında RSA-2048’i kırmanın mümkün olabileceğini söylememişler. Bunu, zaman içinde test edilmiş iki strateji aracılığıyla yapmaları gerekiyor;
1) Ayrıntılı analiz yapılmaması (çoğunlukla, kapı sayısını göz ardı ederken qubit sayısının optimizasyonu),
2) Algoritmanın kuantum hızlandırmasının, QAOA’nın belirsiz yakınsaması nedeniyle belirsiz olduğu belirtilmemesi.
Sonuç olarak doğru olmayabilir ama açıkça yanlış da değil. Paniğe gerek yok.
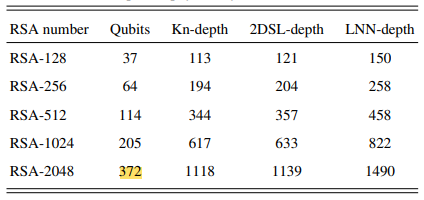
Makalede RSA seviyesi ile qubit seviyesi tanımlanmış ve RSA-2048’yi bu yöntemle kırmak 372 qubit gerektiği hesaplanmış (Bölüm E. “E. Resource estimation for RSA-2048”)
Sonuç olarak;
- Araştırmacılar eş değer sistemlerde (örneğin IBM Osprey ile) işlemi tekrarlayabilir/doğrulayabilir,
- Çin hükümeti makaleyi sınıflandırabilir.
Bu gerçekleştiğinde 372-qubit sisteme erişimi olan kişiler RSA-2048 seviyesini kırabilecek. RSA algoritması kırılma koşulu belirleneceği üst seviye bitler için iş donanıma kalacak. Ancak bu hipotez gerçekleşirse başka/birleştirilmiş kırma tekniklerini beraberinde getirebileceğini tahmin etmek güç olmaz… (Matematik, Fizik..)…